und ihre Bestimmung
Zu Beginn der Astronomie war nur der sichtbare Spektralbereich (400 bis 750 nm) zugänglich. Erst mit dem technischen Fortschritt ab etwa 1950 kamen auch die anderen Bereiche hinzu.
|
In der Tabelle sind die physikalisch messbaren Zustandsgrößen eines Sterns und das Meßverfahren gegenüber gestellt. Die Nummern rechts entsprechen den Kapiteln auf dieser Seite. |
1. Leuchtkraft, Helligkeit, Farbe
Bei der Sonne kann die Leuchtkraft direkt bestimmt werden (Bolometer). Das ergibt für die Gesamtleistung auf der Gesamtfläche der Kugel mit dem Radius der Erdbahn eine Leistung von 3,9 x 10E33 erg/sec.
1.1 scheinbare HelligkeitDie scheinbare Helligkeit ist die älteste Größe, mit der ein Stern beschrieben wird und keine echte Zustandsgröße, da sie ein Wert ist, der von der Entfernung des Sterns abhängt. |
1.2 FarbindexEr ist die Differenz zwischen der in zwei verschiedenen Bereichen des Spektrums gemessenen Helligkeit. |
1.3 absolute Helligkeit, Leuchtkraft
Die absolute Helligkeit wird mit einem M angegeben und entspricht der scheinbaren Helligkeit, die ein Stern besäße, wenn er sich in einer Entfernung von zehn Parsec (32,6 Lichtjahre) zur Erde befände. Dadurch erhält man ein für jeden Stern vergleichbares Maß der Helligkeit. Dies ermöglicht den Vergleich unterschiedlicher Sterne bezüglich ihrer Helligkeit. Die Sonne besitzt eine absolute Helligkeit von +4,83.
Leuchtkraft ist die Strahlungsleistung eines Sterns und beschreibt seine gesamte pro Zeiteinheit abgestrahlte Energie, die in der Astronomie mit der Einheit Erg/sec angegeben wird.
In bestimmten Zusammenhängen kann es praktisch sein, andere Einheiten wie zum Beispiel „Sonnenleuchtkräfte“ zu verwenden.
Die Leuchtkraft der Sonne beträgt 1370 Watt pro mE2, das ist die auf die Erde auftreffende Leistung. Dazu muss die Energie berechnet werden, die an der Oberfläche einer Kugel mit dem Radius der Entfernung Erde – Sonne ankommt.
2 Temperatur
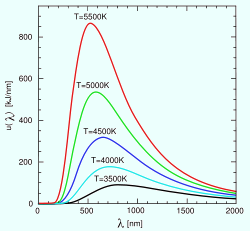
| Die effektive Temperatur (Oberflächentemperatur) bestimmt die Farbe des Sterns. So erscheint uns ein kühler Stern mit nur 3000° rot, ein heißer Stern mit einer effektiven Temperatur von 10 000° leuchtet blau. Zur Bestimmung der effektiven Temperatur eines Sterns dient sein Spektrum. Aus der Lage des Intensitätsmaximums erhält man (nach dem Wienschen Verschiebungsgesetz, Bild rechts) die Temperatur der strahlenden Oberfläche. Das Wien´sche Verschiebungsgesets beschreibt den Zusammenhang zwischen Temperatur und abgestrahlter Wellenlänge. Die Temperatur der Sonnenoberfläche (Photosphäre) beträgt 5600°C, die Temperatur im Innern beträgt dagegen 15 Millionen Grad. |
 |
3. Masse
Sternmodelle sagen voraus, dass die Temperatur des Sternes mit der Masse korreliert und somit Leuchtkraft und Masse. Einfache Sternmodell, beruhend auf Formeln des idealen Gase, des Stahlungstransports über Absorption und Emission, sagen einen proportionalen Zusammenhang von Leuchtkraft und der Masse voraus (
Die Masse der Sonne beträgt 2 x 1030 kg .
3.1 Doppelsterne
| Eine direkte Messung ist nur bei Doppelsternen möglich. Aus dem Abstand der Sterne vom gemeinsamen Schwerpunkt und der Umlaufdauer erhält man nach dem 2. Keplerschen Gesetz die Summe beider Massen. M1 + M2 = a3 / p2 Und aus M1 / M2 = a2 / a1 die einzelne Masse. Bei diesen Formeln bedeutet: M = Masse, a = die große Halbachse der Umlaufbahn, p = Umlaufzeit in Jahren. Es kann auch die Umlaufgeschwindigkeit (Dopplereffekt) einer Komponente gemessen werden. Aus der Geschwindigkeit und dem Abstand vom gemeinsamen Schwerpunkt (aus der Pendelbewegung der beiden Komponenten), lässt sich mit Hilfe des Gravitationsgesetzes die Masse der zweiten Komponente berechnen. Der Bereich der Sternmassen liegt zwischen 0,08 und 100 Sonnenmassen. |
3.2 Masse-Leuchtkraft-Beziehung
| Aus dem Hertzsprung-Russel-Diagramm ist die Beziehung, die für Hauptreihensterne gilt, zu ersehnen. Die Leuchtkraft ist korreliert mit der Temperatur, denn alle Sterne liegen auf einer Linie. Sternmodelle sagen voraus, dass die Temperatur des Sternes mit der Masse korreliert und somit Leuchtkraft und Masse. Einfache Sternmodell, beruhend auf Formeln des idealen Gase, des Stahlungstransports über Absorption und Emission, sagen einen proportionalen Zusammenhang von Leuchtkraft und der Masse voraus (L ~ M2). Gemessen wird für Sterne der Popultion I L ~ M285 , was recht gut mit der Theorie übereinstimmt. Die Masse der Sonne beträgt 2 x 1030 kg . |
4. Radius
Der Radius eines Sterns verändert sich im Laufe seines Lebens. Er liegt im Bereich von 5 bis 10 km (bei Neuronensternen) und bis zu 300x10E6 km (bis zu 450-fachem Sonnenradius bei delta Cepheiden, 315x10E6 km).
Der Radius der Sonne beträgt 700 000 km. Als „Oberfläche“ wird die Photosphäre angenommen.
Folgende Methoden sind möglich:
4.1 Interferometer
| Abbildung 1 (rechts) zeigt den optischen Aufbau des Interferometers am Mount Wilson. Die zwei Spiegel S1 und S2 konnten symmetrisch zur optischen Achse O verschoben werden und somit die Distanz d geändert werden. Das mit Hilfe der Teleskopoptik zusammengeführte Sternenlicht kommt im Fokus zur Interferenz. Diese Interferenzerscheinungen kann man anhand der Abbildung 2 und 3 veranschaulichen. | 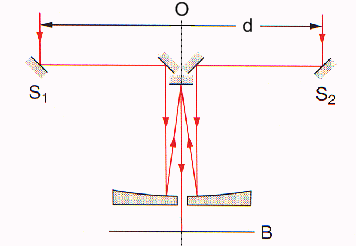 |
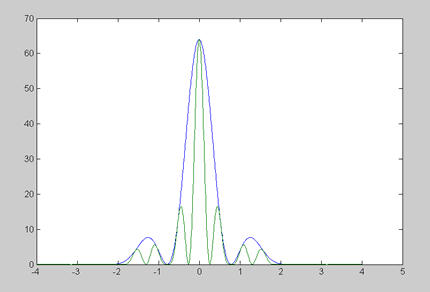 |
Abbildung 2 (links) zeigt die Interferenzstrukturen für 2 Spiegel mit einer Entfernung von 1m und einem eigenem Durchmesser von 30cm. Die feinen Interferenzstrukturen kommen von der Spiegeldistanz und die Spitzen haben eine Distanz in erster Näherung von 0.11“ (nach der Formel Winkel = 112 / (Durcmesser Optik in mm)). Die grobe einhüllende Struktur wird verursacht durch die begrenzte Apertur der Hilfsspiegel und hat eine Breite bis zum ersten Minimum von 0.37“. |
| Abbildung 3 (rechts) zeigt die Beugungsstrukturen für eine Spiegelentfernung von 5m. Deutlich wird, dass sich die einhüllende Kurve unverändert ist (wird ja durch die Öffnung der Hilfspiegel verursacht, die sich nicht geändert haben), aber die Substrukturen haben jetzt einen Faktor 5 kleineren Winkelabstand von 0.022“. | 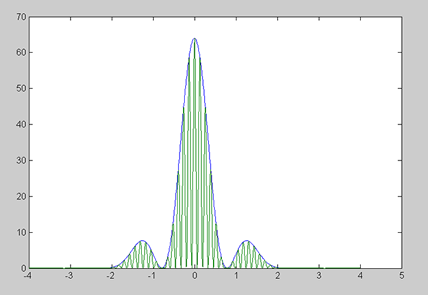 |
| Nehmen wir an, dass der Stern sich um einen kleinen Winkel verschiebt (z.B. durch Nachführungsfehler), so verschiebt sich das gesamte Interferenzmuster um den gleichen Betrag. Hat der Stern jetzt eine endliche Winkelausdehnung, so produziert jeder Punkt seiner Oberfläche des Sternscheibchens ein verschobenes Interferenzmuster. Hat der Stern zum Beispiel den gleichen Winkeldurchmesser wie der Winkeldurchmesser der Beugungsstrukturen, welche durch die Spiegelentfernung verursacht werden, so verschwinden die Interferenzstrukturen. Dies kann man sich wie folgt vorstellen: Die meisten Punkte auf der linken Sternhälfte finden einen Partner mit Abstand des Sternwinkelradiuses auf der rechten Sternhälfte. Da dieser Winkelabstand dem Winkel zwischen Maximum und Minimum der Beugungsstruktur entspricht überlagern sich die beiden Signale und ergeben ein mittleres Signal, welches keine Berge und Täler aufweist. | Folglich wird zum Beobachten die beiden Spiegel zuerst mit kleiner Distanz eingesetzt und die Interferenzstrukturen beobachtet. Dann fährt man die Spiegel solange auseinander, bis die Interferenzstrukturen sich aufheben (Winkelkohärenz ist aufgehoben). Diese Spiegeldistanz beschreibt den Winkel des Sternesradius. Grenze dieser Methode ist die maximale Spiegeldistanz, bei Mount Wilson waren es 6m und damit 0.018“. Beteigeuze wurde als erster Stern vermessen (13.12.1920, Bernham´s celestial handbook) mit einem Winkel von ca. 0.044“. Dies entspricht bei einer Entfernung von 520 Lichtjahren einem Radius von 10E9 km, was ca. dem 7 fache Erdbahnradius entspricht. Damit gehört Beteigeuze zu einem der größten Sterne und ist der größte Stern den man mit bloßem Auge sehen kann. |
4.2 Sternbedeckung durch den Mond
Ein punktförmiger Stern verschwindet schlagartig hinter dem Mond, da dieser keine Atmosphäre besitzt. Ein Stern mit merklichem Radius verschwindet dagegen allmählich. Aus dem Verlauf des Helligkeitsabfalls folgt der Radius. Die Messgrenze liegt bei 0,002 Sekunden.
4.3 Bedeckungsveränderliche
| Aus der Lichtkurve erhält man die Radien beider Komponenten in Abhängigkeit von der Bahnlänge. Durch spektroskopische Beobachtungen kann die Bahngeschwindigkeit (Dopplereffekt) gemessen werden. Voraussetzung ist, dass die Bahnebene in der Sichtlinie liegt. Je größer die Abweichung davon, umso größer ist der Fehler. Daraus folgen Bahnlänge und die Radien beider Komponenten in linearem Maß. | 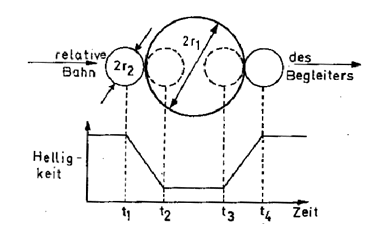 |
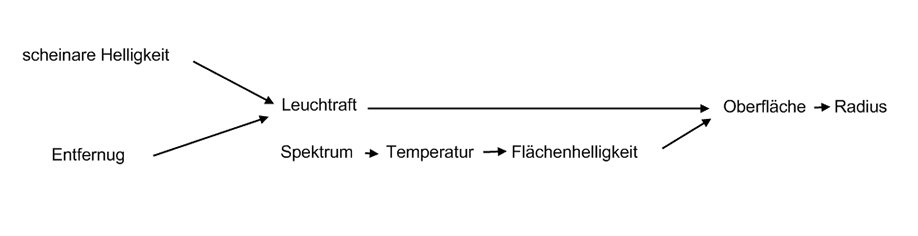
4.4 Strahlungsenergetische Methode
Aus der scheinbaren Helligkeit und der Entfernung erhält man die Leuchtkraft (gesamt ausgestrahlte Energie). Aus dem Spektrum ergibt sich über die Temperatur die Flächenhelligkeit. Mit Hilfe von Leuchtkraft und Flächenhelligkeit lassen sich die strahlende Oberfläche und damit der Radius berechnen.
5. chemische Zusammensetzung
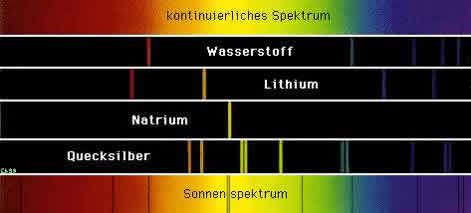
Elektromagnetische Strahlung kann mit Hilfe von Spektralapparaten zerlegt werden. Das einfachste Grundelement dieser Instrumente ist das Prisma. Glas bricht blaues Licht stärker als rotes. Man erhält so das sichtbare Spektrum aufgespaltet von blau bis rot.
Joseph von Fraunhofer entdeckte 1814 im Sonnenspektrum dunkle Linien, die Fraunhofersche Linien genannt werden, denen er jedoch keinen Entstehungsmechanismus zuordnen konnte. Jedes Atom eines Elements sendet diskrete Wellenlängen aus, die aus den Übergängen der Elektronen berechnet werden können (1861 entdeckt von Kirchhoff und Bunsen). Diese Tatsache spiegelt sich in den Linien des Spektrums wieder.
Je nach Entstehungsart des Wellengemischs unterscheidet man Emissions- und Absorptionsspektrum.
5.1 Absorptionsspektrum
| Ein Absorptionsspektrum entsteht durch Absorption ganz bestimmter Wellenlängen bzw. Frequenzen. In diesem Fall absorbieren die Atome aus einem kontinuierlichen Spektrum praktisch die Wellenlängen, die es bei Anregung auch selbst emittieren würden. Damit dies geschieht, muß das absorbierende Atom zwischen Beobachter und beobachteter Strahlungsquelle liegen. So befindet sich die Korona der Sonn zwischen Photosphäre und Beobachter. Sie verursacht die typischen Absoptionslinien im Sonnenspektrum. | |
Absorptionslinien des Heliums |
|
| Man erhält von der Sonne ein Absorptionsspektrum. Das Licht geht von der Photosphäre aus, darüber liegen Chromosphäre und die dünne, heiße Korona, die bei Sonnenfinsternissen zu sehen sind. Diese beiden Schichten absorbieren Teile des kontinuierlichen Spektrums, welches von der Photosphäre ausgeht. So werden die Fraunhoferschen Linien herausgeschnitten. Bereits 1868 wurde Helium (von P.J.C.Janssen) entdeckt, allerdings nicht auf der Erde, sondern durch die Beobachtung und Interpretation des Sonnenspektrums. Dieses enthielt einige Linien, die keinem bis dahin bekannten Element zuzuordnen waren. Das neue Element wurde nach der Sonne (griechisch „Helios“) benannt. Erst Jahrzehnte später (1895 von W.Ramsay) wurde Helium auch auf der Erde gewonnen |
5.2 Emissionsspektrum
| Im Gegensatz dazu wird ein Emissionsspektrum von Atomen ausgesandt, die zum Aussenden von Strahlung angeregt wurden, das heißt ein Elektron fällt auf eine niedrigere Bahn und sendet Strahlung einer bestimmten Wellenlänge aus. Es entstehen helle Linien. Diese Spektren beobachtet man bei Gasnebeln, die von nahen Sternen zum Leuchten angeregt werden. Dieses Emissionsspektrum wird auch an Protuberanzen der Sonne beobachtet. Diese Materieauswürfe liegen vor dunklem Hintergrund am Sonnenrand. |
|
 |
6. Rotation
Eine einfache und genaue Messung ist nur bei der Sonne durch Beobachtung von Oberflächenstrukturen möglich (Flecken). Bei anderen Sternen können spektroskopische Methoden nur in gewissen Konstellationen angewandt werden.
6.1 Dopplereffekt
| Bei einigen Bedekungsveränderlichen gibt es die Möglichkeit, wenn kurzzeitig nur der rechte oder linke Sternrand sichtbar ist, kann mit Hilfe des Dopplereffekts die Geschwindigkeit des Sternrandes gemessen werden. (Das Licht, dass vom sich entferneden Sternrand ausgesandt wird, ist in Richtung rotes Spektrumsende verschoben, die Lichtwelle wird durch die Bewegung weg vom Beobachter "in die Länge gezogen".) Diese Messung ergibt nur dann die tatsächliche Geschwindigkeit des Sternrandes wenn die Rotationsachse senkrecht auf der Sichtlinie Erde-Stern steht. Es gibt keine Möglichkeit die Lage der Rotationsachse festzustellen. Sie sollte nicht mehr als 10 Grad geneigt sein weil sonst der Fehler zu groß ist. |
6.2 Linienverbreiterung
| Bei Einzelsternen kann die Messung der Verbreiterung der Spektrallinien Auskunft über den Rotation geben. Ein Sternrand bewegt sich auf uns zu (Spektrallinien zum blauen Ende verschoben), der andere entfernt sich von uns (Rotverschiebung). Die Spektrallinien, die uns von der Sternmitte erreichen, weisen keine Verschiebung auf. Dadurch ergibt sich die Verbreiterung der Spektrallinien. Die Sonne hat eine differentielle Rotation: an den Polen 28 Tage und am Äquator 25 Tage. |
7. Magnetfeld
Aufgrund subatomarer Effekte wird die Spektrallinie durch ein Magnetfeld aufgespaltet (Zeemann-Effekt). Bei schwachen Magnetfeldern werden die Spektrallinien nur verbreitert. Man muss hier von der Rotationsverbreiterung unterscheiden.
Magnetfeld der Erde: 10E-5 Tesla, das der Sonne 10E-4 Tesla, bei Neutronensterne treten bis zu 10E11 Tesla auf.
Hier ist allerdings Vorsicht geboten, denn eine Verbreiterung der Spektrallinien kann auch andere Ursachen haben. So zum Beispiel Rotation oder Druck.